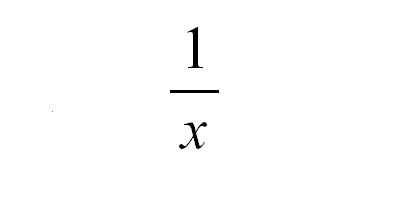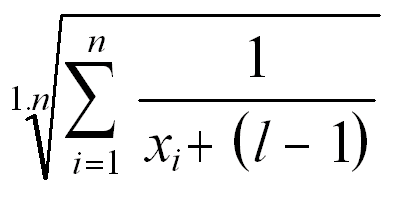Difference between revisions of "Val's Wacky Equation"
Gpfontaine (talk | contribs) m (All images uploaded and entered. Still needs formatting though.) |
Gpfontaine (talk | contribs) m |
||
| Line 4: | Line 4: | ||
== The Equation == | == The Equation == | ||
| − | Those of you who have read through the Top 100 SNES list, and possibly the Top 100 NES list, might be wondering how we came to the final ordering for these games. Well, each game received a score from 1 to 1000 based on it's position on each individual list, and was then ranked against all other games with the highest scoring game getting the top spot. | + | {{Quote |
| + | |quote= Those of you who have read through the Top 100 SNES list, and possibly the Top 100 NES list, might be wondering how we came to the final ordering for these games. Well, each game received a score from 1 to 1000 based on it's position on each individual list, and was then ranked against all other games with the highest scoring game getting the top spot. | ||
| + | |author= [[Valdronius]] | ||
| + | }} | ||
| + | === Simple Version .... LOL You won't understand it === | ||
Now you may be wondering how each games score was calculated. Well, to put it simply: | Now you may be wondering how each games score was calculated. Well, to put it simply: | ||
| − | + | ||
<div align="center">[[Image:ValRank0.png]] | <div align="center">[[Image:ValRank0.png]] | ||
| Line 14: | Line 18: | ||
x is the game's position on an individual list, | x is the game's position on an individual list, | ||
| + | and l is the total number of individual lists.</div> | ||
| − | + | === Breaking down the equation === | |
| − | + | For those of you who haven't taken university mathematics, I shall go into a more detailed explanation of each step along the way. (For those of you who have, I apologize for using 1.n, it just looks nicer than 1 + n/10). | |
| − | |||
| − | For those of you who haven't taken university mathematics, I shall go into a more detailed | ||
| − | Alright, let's start from the inside and work our way out. For clarity, from here out when I use the term 'rank', I'm | + | Alright, let's start from the inside and work our way out. For clarity, from here out when I use the term 'rank', I'm referring to a games rank on an individual list. |
<div align="center">[[Image:ValRank1.png]]</div> | <div align="center">[[Image:ValRank1.png]]</div> | ||
| − | The first thing we do is take the | + | The first thing we do is take the [http://www.mathwords.com/m/multiplicative_inverse_of_a_number.htm reciprocal] of the games rank. If I rated one game 15th on my list, and another game 30th, it wouldn't make sense to give them 15 points and 30 points respectively, as we wanted the 15th ranked game to be higher on the final list. So we take the reciprocal of each number to achieve the desired result. 1/15 = 0.067, 1/30 = 0.033. |
| − | |||
<div align="center">[[Image:ValRank2.png]]</div> | <div align="center">[[Image:ValRank2.png]]</div> | ||
| − | + | ||
Before we take the reciprocal, we want to add what I call a 'limiter' to the games rank. The limiter is the total number of individual lists, less 1. It might not be immediately clear why this is necessary, so let's move forward. | Before we take the reciprocal, we want to add what I call a 'limiter' to the games rank. The limiter is the total number of individual lists, less 1. It might not be immediately clear why this is necessary, so let's move forward. | ||
| Line 51: | Line 53: | ||
So that's how the ranking system was designed. I hope someone out there enjoyed reading this. | So that's how the ranking system was designed. I hope someone out there enjoyed reading this. | ||
| + | |||
== Why Averaging Isn't a Good Option == | == Why Averaging Isn't a Good Option == | ||
Revision as of 06:23, 24 November 2008
Have you ever wondered how Val's mind works?
Well, he gave us some insight when he explained how the top 100 NES & SNES games were ranked.
Contents
The Equation
| Those of you who have read through the Top 100 SNES list, and possibly the Top 100 NES list, might be wondering how we came to the final ordering for these games. Well, each game received a score from 1 to 1000 based on it's position on each individual list, and was then ranked against all other games with the highest scoring game getting the top spot. | ||
| - Valdronius |
Simple Version .... LOL You won't understand it
Now you may be wondering how each games score was calculated. Well, to put it simply:

Where n is the number of individual lists the game appeared on,
x is the game's position on an individual list,
and l is the total number of individual lists.Breaking down the equation
For those of you who haven't taken university mathematics, I shall go into a more detailed explanation of each step along the way. (For those of you who have, I apologize for using 1.n, it just looks nicer than 1 + n/10).
Alright, let's start from the inside and work our way out. For clarity, from here out when I use the term 'rank', I'm referring to a games rank on an individual list.
The first thing we do is take the reciprocal of the games rank. If I rated one game 15th on my list, and another game 30th, it wouldn't make sense to give them 15 points and 30 points respectively, as we wanted the 15th ranked game to be higher on the final list. So we take the reciprocal of each number to achieve the desired result. 1/15 = 0.067, 1/30 = 0.033.
Before we take the reciprocal, we want to add what I call a 'limiter' to the games rank. The limiter is the total number of individual lists, less 1. It might not be immediately clear why this is necessary, so let's move forward.
The next step is to add up all those reciprocals from the individual lists. The more lists a game appears on, and the higher its rank, the higher this number will be. This is also where the limiter becomes important. Let's say there were 5 lists, and everybody voted a certain game #1. Then we'd have this happening:
So the highest possible total a game can have a this point is 1. Without the limiter, a game could have a score higher than 1 at this point, which would cause some wonky things in the next step.
Finally we have a booster. When a game appears on multiple lists, it gets a boost for the number of lists it appears on. So again, if there are 5 lists, a game could receive a low boost of 1.1 for being on 1 list, up to 1.5 for appearing on 5 lists. If you want to see why I had to use the limiters, take the 1.5th root of 2, and the 1.1th root of 2. For this system we would want the former to be higher, but you'll see that this is not the case. When the numbers are between 0 and 1, this achieves the desired effect.
Well, that was fairly long-winded. Let's walk through an example to see how A Link to the Past scored. There were 7 lists in total, and it was ranked 6, 1, 1, 4, 2, 2, and 4. Then we'll get this:
Multiplying the number at the end by 1000 is purely for aesthetic reasons. It is easier to rank numbers that range from 1 to 1000 than it is to rank numbers ranging from 0 to 1. To show that the booster does indeed work the way it is supposed to, let's take the 1.1th root of 0.8190476. This results in 0.834 or a score of 834.
So that's how the ranking system was designed. I hope someone out there enjoyed reading this.