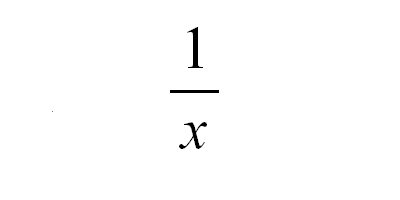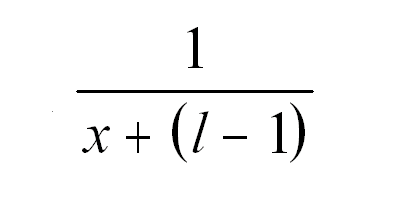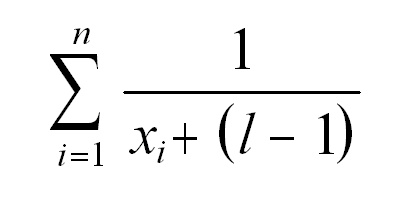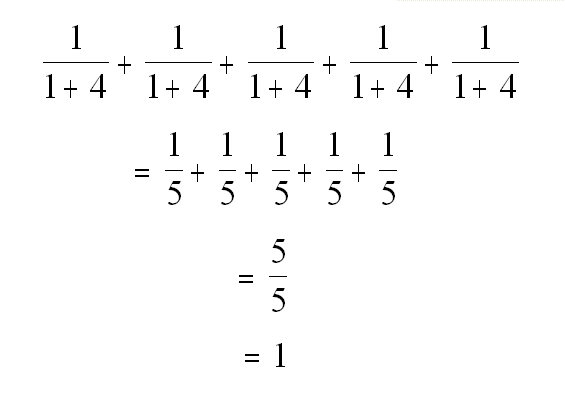Val's Wacky Equation
Have you ever wondered how Val's mind works?
Well, he gave us some insight when he explained how the top 100 NES & SNES games were ranked.
Contents
The Equation
| Those of you who have read through the Top 100 SNES list, and possibly the Top 100 NES list, might be wondering how we came to the final ordering for these games. Well, each game received a score from 1 to 1000 based on it's position on each individual list, and was then ranked against all other games with the highest scoring game getting the top spot. | ||
| - Valdronius |
Simple Version .... LOL You won't understand it
Now you may be wondering how each games score was calculated. Well, to put it simply:
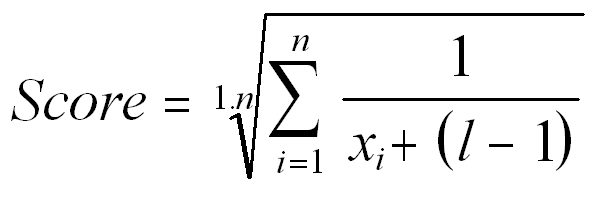
Where n is the number of individual lists the game appeared on,
x is the game's position on an individual list,
and l is the total number of individual lists.Breaking down the equation
For those of you who haven't taken university mathematics, I shall go into a more detailed explanation of each step along the way. (For those of you who have, I apologize for using 1.n, it just looks nicer than 1 + n/10).
Alright, let's start from the inside and work our way out. For clarity, from here out when I use the term 'rank', I'm referring to a games rank on an individual list.
The first thing we do is take the reciprocal of the games rank. If I rated one game 15th on my list, and another game 30th, it wouldn't make sense to give them 15 points and 30 points respectively, as we wanted the 15th ranked game to be higher on the final list. So we take the reciprocal of each number to achieve the desired result. 1/15 = 0.067, 1/30 = 0.033.
Before we take the reciprocal, we want to add what I call a 'limiter' to the games rank. The limiter is the total number of individual lists, less 1. It might not be immediately clear why this is necessary, so let's move forward.
The next step is to add up all those reciprocals from the individual lists. The more lists a game appears on, and the higher its rank, the higher this number will be. This is also where the limiter becomes important. Let's say there were 5 lists, and everybody voted a certain game #1. Then we'd have this happening:
So the highest possible total a game can have a this point is 1. Without the limiter, a game could have a score higher than 1 at this point, which would cause some wonky things in the next step.
Finally we have a booster. When a game appears on multiple lists, it gets a boost for the number of lists it appears on. So again, if there are 5 lists, a game could receive a low boost of 1.1 for being on 1 list, up to 1.5 for appearing on 5 lists. If you want to see why I had to use the limiters, take the 1.5th root of 2, and the 1.1th root of 2. For this system we would want the former to be higher, but you'll see that this is not the case. When the numbers are between 0 and 1, this achieves the desired effect.
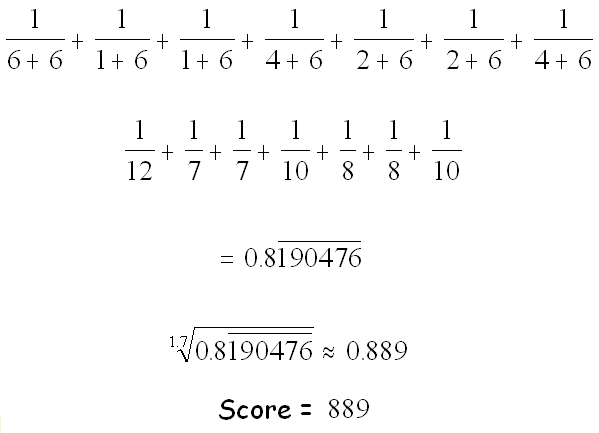
Well, that was fairly long-winded. Let's walk through an example to see how A Link to the Past scored. There were 7 lists in total, and it was ranked 6, 1, 1, 4, 2, 2, and 4. Then we'll get this:
Multiplying the number at the end by 1000 is purely for aesthetic reasons. It is easier to rank numbers that range from 1 to 1000 than it is to rank numbers ranging from 0 to 1. To show that the booster does indeed work the way it is supposed to, let's take the 1.1th root of 0.8190476. This results in 0.834 or a score of 834.
So that's how the ranking system was designed. I hope someone out there enjoyed reading this.
Why Such An Elaborate System?
Simpler systems simply don't work. At least, for what we were trying to accomplish, they didn't achieve the desired effect.
Reverse Point System
This was talked about a lot early on in the NES list process. Namely, this system would give 100 points to the game ranked #1 on someones list, 99 points for the #2 game, and so forth, giving 1 point for the #100 game.
This very nearly won out for the system to use, but I objected because I felt it wasn't accurate. For example, if all five people involved in the NES project had picked the same game as their #100, it would only receive 5 points, and would be beaten out by a game that one person placed at #95. It was a general consensus that a game everybody thought was top 100 material should be given more weight than a game that one person threw into their bottom 10.
The Equation above accounts for this. In fact, if five people ranked a particular game in the #100 spot, it would receive a higher score than a game that one person ranked at #5. This might seem like an injustice, but it really isn't, as I will further explain.
Averaging
Another idea that was suggested after the fact was averaging. For example, if a particular game was ranked #12, #19, and #20, we take the average of those three numbers and place it around #17. The biggest problem with this method is that if some idiot feels that Rex Ronan: Experimental Surgeon is the best game on the SNES, it's average is going to 1, and suddenly we are publishing a list with Rex Ronan as the best SNES game of all time. One person might really enjoy a particular game, but that doesn't mean that it is one of the best SNES games. The Equation solves this problem.
Furthermore, if two people think a particular game is top 20 material, it will have an average in the top 20. If everyone feels that another game is top 25 material, its average would like be in the low 20's. For the purposes of this project, we wanted the unanimously good game to beat out the game that two people enjoyed.